CMO/OAA Cahier #03
1990 - 331=1659
|
It |
is usually said that the planet
Mars approaches the Earth every two years
and two months, but the succeeding Mars does not appear the same with
the preceding one in the sense that the Martian season is deviated from the
preceding one, not to mention the apparent disk diameter.
The
planet is however known to show periodically its similar surface or season if
we shall wait every 15 years or 17 years. For example, the year 1988 of the
preceding favourite opposition minus 17 yields 1971, and 1971 minus 15 makes
1956, which were all the years of the 'great' apparitions. These 'most'
favourite apparitions turned out however to be not quite the same one another.
It is really not easy, or it will take a longer time (longer than 15, 17, or
15+17 =32), to have the recurrence of the same season of the planet Mars seen
from the same orbital site of our planet Earth. The reason why it is usually
difficult to watch the planet at a certain point on the Martian orbit from
another fixed site on the terrestrial orbit is because the usual combinations
of such quantities as the Mean Synodic Period of
Mars, denoted here by P, and the
Sidereal Period of the Earth, denoted by Q, cannot be expressed easily by the rational numbers.
Our
purpose here is to find out plausible years of recurrence by a simple,
arithmetical consideration. (This method was found by the present writer, and
originally published in The Heavens (OAA Journal 65 (1984) 187 in Japanese.)
First
note that P – 2Q gives the days which a twice encircling of the Earth around the
Sun needs further to reach the Synodic Period. If an integer
multiple of this additional days gives another integer multiple of Q, then a recurrence will certainly
occur. Hence if an exact periodicity exists, we should first have
m×Q = n×(P –
2Q), (1)
where n, m are arbitrary positive integers. Equation (1) is alternatively
written as
Q/(P –
2Q) = n/m. (2)
Here n/m is a rational number, but in reality we will encounter possibly
an irrational number for the lhs of
(2), and hence Eq.(2) must be no more than an
approximation.
Our
next proposition is to assert that 2n +m gives a year of recurrence when Eq.(2) holds. To see this we have only to rewrite Eq.(2) as
(2n+m)Q = nP. (3)
That is, 2n+m times Q is now proportional
to P, and hence 2n + m is apparently a recurrence year.
Actual
values of Q and P are given by Q=365.256,
P=779.94 respectively (cf. e.g. The Handbook of the BAA, 1991. p99) and
hence the lhs of (2) reads
Q/(P – 2Q) = 7.390...., (4)
which
will never turn to be rational. Hence we here pick out several
plausible approximations to reality: First if we put n/m equal to the rational number 739/100, then it
must be a very good approximation to (4), but the year of recurrence turns to
be 2n+m=1578, which is however too
large.
Hence
we have to try to derive more realistic numbers from 739/100 = 147.8/20. It is
apparent that n/m = 148/20 comes near
the above value, giving the recurrence year of 316 (= 2×148+20). The ratio
148/20 is however reducible to 37/5, and hence the 316 year periodicity is of
the sane accuracy as the 79 year periodicity (79=2×37+5). This recurrence was
once used in CMO #085.p718.
Instead
of 148/20, we can also pick out 140/19=7.368…or 155/21=7.381…. as possible
approximations. The former one will give
|
163 22
7.400. . . 348 155 21
7.380. . . 331 148 20
7.400. . . (316) 141 19
7.421 . . . 301 133 18 7.388 . . . 284 126 17
7.411 . . . 269 118 16
7.375 . . {252} 111 15
7.400 . . .(237) 103 14
7.357 . . . 220 96
13 7.384 . . . 205 89 12
7.416. . . 130 81
11 7.363 . . . 173 74
10 7.400 . . .(158) 67
9 7.444 . . . 143 66 9 7.333 . .
<141> 59 8 7.375. . . {126} 52 7 7.428. . . 111 44
6 7.333 . . .<94> 37
5 7.400 . . . (79) 30 4 7.500 . .
>64< 29
4 7.250 . . . 62 22
3 7.333 . . .<47> 15
2 7.500 . . . >32< -------------------------------- 14 2
7.000 . .. . 30 8 1
8.000. . . 17 7 1
7.000. . . 15 |
299
years, and the latter 331 years. In
this way we can calculate and obtain possible recurrence years as shown in the
Table. As is easily seen the 284 year periodic recurrence may be said the best.
On the contrary the usual 15 year periodicity is said to be quite rough because
its n/m is only 7.000. As well 17
year one gives too big n/m=8.000. The
first plausible approximation is so the 79 Earth years.
From
the Table, let us tentatively pick out the case of 59/8=7.375 giving 126. Note
that this is also a better approximation. This value tells us a certain year
which resembles the last apparition in 1990/91. Since 1900 minus 126 gives
1864, the apparition in 1864/65 must have been quite the same as 1990/91.
Fortunately, R McKIM and R A MARRIOTT wrote an interesting
article entitled “Dawes' s Observations
of Mars, 1864-65” in JBAA 98 (1988) 294, and in it they reproduced 16 numbers of W R DAWES'
precious drawings in 1864/65, 8 out of 16 being newly published by the article.
(Furthermore they are not the lithogragh copies, but
the photo copies of the faithful copies by DAWES himself of the originals in
his sketchbook!) DAWES' drawings are excellent showing several 
known
markings as well as the temporary markings such as Hydaspes
(developed between 1852 and 1871. Out of all, however, they show clearly the
existence of the varying north polar hood, and especially the one taken on 15
November 1864 at 00:00 GMT (in new GMT system used since 1925) reproduces a
part of M Acidalium (new nomenclature since SCHIAPARELLI) inside the nph as an
isolated dark segment! This must have been the same scene as the view we caught
on 22 October 1990 from
Another
example of the year which is reminiscent of the last apparition in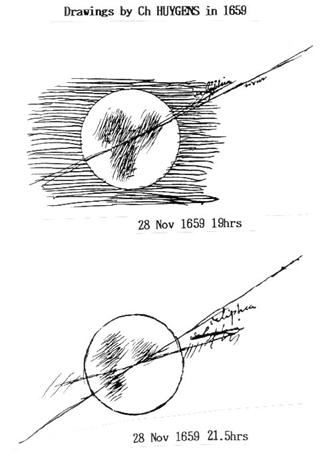 
1990
is 1659, which is derived by subtracting 331 (see the Table) from 1990. The
year 1659 is memorable in the sense that a big marking was first found on the
Martian surface by Christiaan HUYGENS (1629 - 1695).
The value 7.380 associated with 331 is also one of better approximations, and
so the Martian season in 1659 can be thought as having gone through quite the
same way as in 1990. As cited all here from his Œuvres complètes
Tome XV, HUYGENS obtained four drawings on 28 Nov and l Dec 1659 at la Haye by the use of a refractor of 21 pieds
7.5 pouces focal length (un pied was 31.39cm at that
time, and hence 21 pieds 7.5 pouces
imply about 680cm) . It is proven thus very natural that he did not see the
south polar cap in 1659 because at this 
season
of the Martian year the spc is invisible. He depicted clearly the spc however
in his latter sketches in 1672, (1672+316 =1988!).
N.B.
According to McKIM and MARRIOTT, DAWES also observed
in 1851/52 from 18 Nov 1851 to 14 Apr 1852. 1852+141=1993, and hence the next
apparition in 1993 is roughly similar to the 1852 case (roughly because
<141> is equivalent to <47>) . Anyway
DAWES must have observed the npc (instead of the nph)
in 1851/52. The years similar to 1993 may be counted as 1961, 1946, 1929, 1931,
1914, 1899, 1882, 1867, 1852, 1835, 1776, 1741, 1709, 1692, 1677, 1662…...
CMO No.106 (25 June 1991 issue) p910
Back to the Index of the
Cahiers
Back to the CMO Home Page
/ Back to the CMO Façade