MHD Simulation of Magnetic Reconnection and Solar Flares
Shibata, K. &
Yokoyama, T.
National Astronomical Observatoy of Japan
Abstract
In this CD-ROM version, we show some movies presented in the
conference Numerical Astrophysics 1998, such as observations
of coronal X-ray jets discovered by
Yohkoh soft X-ray telescope, and the numerical modeling of these
X-ray jets by Yokoyama and Shibata through
2D-MHD numerical simulations of magnetic reconnection occurring
between emerging flux (as a result of the Parker instability) and
overlying coronal magnetic fields.
Yohkoh soft X-ray observations of X-ray jets
X-ray jets have been discovered by the soft X-ray telescope
aboard Yohkoh as transitory X-ray
enhancements with apparent
collimated motion (e.g., see the review by Shibata et al. 1996).
They are associated with small flares (microflares or subflares),
and have the length
a few 10^3 - 4 x 10^5 km (average 1.5 x 10^5 km),
the apparent velocity 10 - 1000 km/s (average 200 km/s), and the lifetime
ranging from a few minutes to more than a few hours.
The temperature of jets (3 - 6 MK)
is comparable to that of
microflares at the footpoints of the jets, and
the kinetic energy is estimated to be 10^{25} - 10^{28} erg.
There are many evidences of magnetic reconnection
in jets;
i.e., change of magnetic field topology at the footpoint active regions,
and so on.
Shibata et al. found two types of the interaction (reconnection)
between emerging flux and coronal field;
the "anemone-jet" type and the "two-sided-loops/jets" type.
The former occurs when emerging flux appears
in coronal holes. In this case,
a jet is ejected in a vertical direction.
On the other hand, the latter occurs
when emerging flux
appears in quiet regions, and
two loop brightenings (or jets) occur in the horizontal
direction at both sides of the emerging flux.
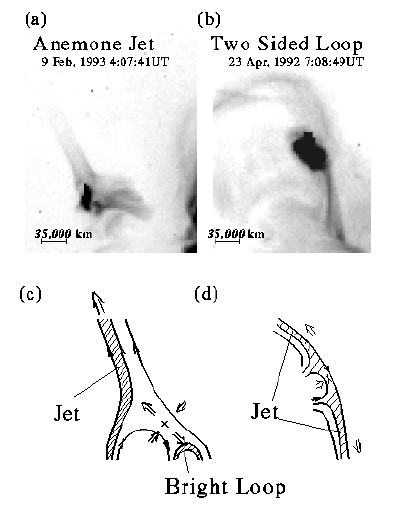
Movie 1: X-ray jet observed by the soft X-ray telescope aboard Yohkoh
(Shibata et al. 1994). This type is called
"anemone-jet" which occurs when emerging flux (rising bipolar magnetic
flux) appears in coronal holes,
where coronal magnetic field fields are open and
nearly vertical or oblique.
The left panel shows positive images, and the right panel shows
negative images. 100" corresponds to 72000 km on the solar surface.
Movie 2: X-ray loop brightening (or horizontal jets)
observed by the soft X-ray telescope aboard Yohkoh
(Shibata et al. 1994, 1998).
This type is called
"two-sided loop (brightenings)"
which occur when emerging flux
appear in quiet regions, where coronal magnetic field fields are closed and
roughly horizontal.
2D-MHD numerical simulations of X-ray jets
Yokoyama and Shibata (1995,1996) performed 2D (and 2.5D) MHD
numerical simulations of magnetic reconnection occurring
in the current sheet between emerging flux and overlying
pre-existing coronal magnetic fields, by extending the simulation
study by Shibata et al. (1992) and applied the results
to X-ray jets ("anemone-jet" and "two-sided-loop") discovered
by Yohkoh. They succeeded to reproduce many observed features
of X-ray jets, such as two types of jets (Movie 1 and 2),
whip-like motion of jets, a gap between the footpoint of a jet
and the brightest part of a footpoint flare, converging shape of jets,
and so on (Shibata et al. 1994, 1996, Shimojo et al. 1996).
It should be noted that the emergence of
magnetic flux (rising motion of magnetic loop) itself is
self-consistently simulated in these numerical simulations.
The basic physics of the emerging flux
(Shibata et al. 1989) is the same as that
of the nonlinear evolution of the Parker instability in galactic
disks (Matsumoto et al. 1988).
The initial condition of these numerical simulations is as follows:
The gas layer consists of three layers (isothermal hot corona
with temperature T = 25 T_0),
isothermal cool chromosphere/photosphere (T = T_0),
and convection zone in the deepest layer)
in magneto-hydrostatic equilibrium under uniform gravity.
The density decreases by more than five decades
from the bottom of the gas layer
to the corona. Initially, horizontal magnetic flux sheet is embedded
in the convection zone just below the photosphere (z < 0), which is unstable
to the Parker instability (undular mode of magnetic buoyancy instability).
The plasma beta (= gas pressure/magnetic pressure) in the initial
flux sheet is 4. On the other hand, nearly uniform horizontal or
oblique magnetic filed is assumed in the corona, where the plasma beta
is 0.2.
The unit of the length and time are H and H/Cs, where
H (= 200 km) and Cs (= 10 km/s) are the pressure scale height and
sound speed in the cool layer (chromospher/photosphere).
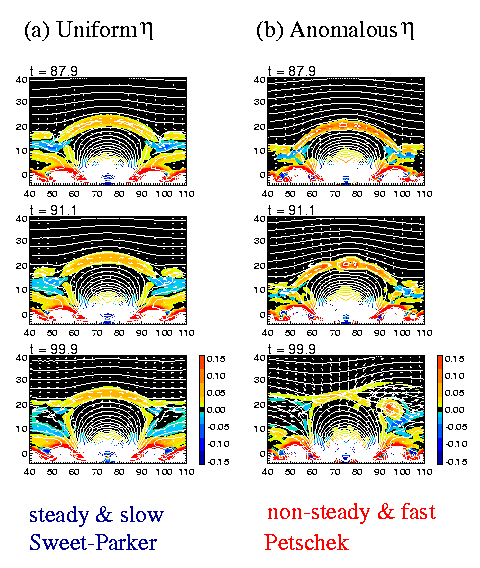
We assume anomalous resistivity model;
eta = eta_0 (v_d - v_c)^2 (for v_d > v_c),
eta = 0 (for v_d < v_c),
where eta is the magnetic diffusivity, v_d = j/rho
is the effective electron - ion drift velocity of the electric
current (j), rho is the mass density, v_c is the critical velocity
(e.g., ion thermal velocity) above which the anomalous resistivity
sets in. The effective magnetic Reynolds number (= L V_A/eta)
is 300 - 3000, where L is the length of the current sheet, and V_A
is the Alfven speed just above the current sheet.
This type of resistivity is essential to model fast
reconnection (Petschek type reconnection) as shown by
Yokoyama and Shibata (1994).
They showed that if we assume
uniform resistivity, the reconnection becomes Sweet-Parker
type even if magnetic reconnection is driven by external force
(magnetic buoyancy force in our case).
Comparison between Uniform Resistivity and Anomalous Resistivity
(Yokoyama and Shibata 1994)
Reconnection Models for Two Types of X-ray Jets
(Yokoyama and Shibata 1995, 1996)
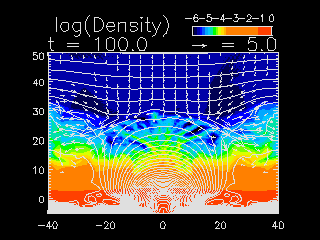
Movie 3: 2D MHD numerical simulations of magnetic reconnection
between emerging flux and overlying coronal field
(Yokoyama and Shibata 1995, 1996). The case of
horizontal coronal magnetic field, as a model of
two-sided loop brightenings type. These figures show the
density
distribution, velocity vectors, and magnetic field lines.
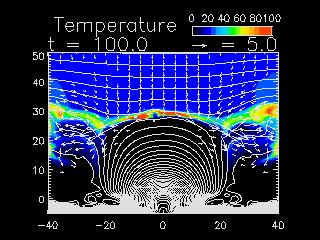
Movie 4: The same as in Movie 3 but for
temperature (Yokoyama and Shibata 1995, 1996).
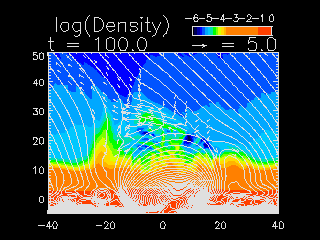
Movie 5: 2D MHD numerical simulations of magnetic reconnection occurring
between emerging flux and overlying coronal field
(Yokoyama and Shibata 1995, 1996). The case of
oblique coronal magnetic field, as a model of anemone-jet type.
These figures show the
density distribution, velocity vectors, and magnetic field lines.
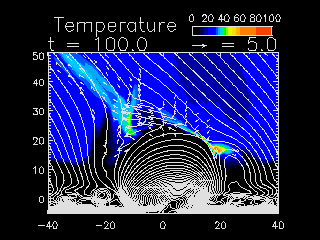
Movie 6: The same as in Movie 5 but for
temperature (Yokoyama and Shibata 1995, 1996).
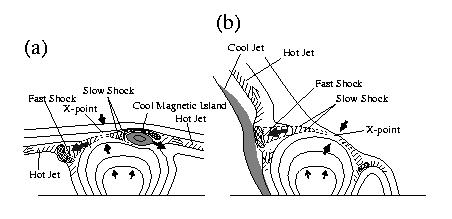
Illustration of Physical Structure of Magnetic Reconnection and
Jets found from Numerical Simulations
Acknowledgements
The authors would like to thank M. Shimojo and S. Yashiro for
preparing movies of X-ray jets and loop brightenings observed
by Yohkoh soft X-ray telescope. The Yohkoh mission is
a project of the ISAS, Japan, with subtantial participation from
other institutions within Japan, and with important contributions
from the research groups in the U.S. and the U.K, under the support
of NASA and SERC.
References
Matsumoto, R., Horiuchi, T., Hanawa, T., and Shibata, K., (1988)
PASJ, 40, 171
Shibata,K., Tajima,T., Steinolfson,R. and Matsumoto,R., (1989)
ApJ, 345, 584
Shibata, K., Nozawa, S., and Matsumoto, R., (1992)
PASJ, 44, 265
Shibata, K., Nitta, N., Strong, K. T., et al. (1994)
ApJ, 431, L51
Shibata, K., Yokoyama, T., Shimojo, M., (1996)
J. Geomag. Geoelectr. , 48 , 19
Shibata, K., Nitta, N., Shimojo, M., and Yashiro, S. (1998)
in preparation.
Shimojo, M., Hashimoto, S., Shibata, K., et al. (1996)
PASJ, 48, 123
Yokoyama, T., & Shibata, K. (1994), ApJ, 436, L197
Yokoyama, T., & Shibata, K. (1995), Nature, 375, 42
Yokoyama, T., & Shibata, K. (1996), PASJ, 48, 353
produced by K. Shibata
in 1998.






